第11章 散列表

一、概念

1.综述

散表表仅支持INSERT、SEARCH、DELETE操作。

把关键字k映射到槽h(k)上的过程称为散列。

多个关键字映射到同一个数组下标位置称为碰撞。

好的散列函数应使每个关键字都等可能地散列到m个槽位中

2.散表函数

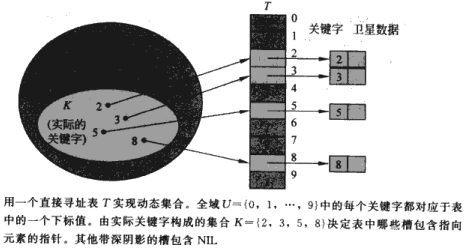
（1）若函数为h(k)=k，就是直接寻址表

（2）除法散列法：h(k) = k mod m

（3）乘法散列法：h(k) = m (k A mod 1) (0<A<1)

（4）全域散列：从一组仔细设计的散列函数中随机地选择一个。（即使对同一个输入，每次也都不一样，平均性态较好）

3.冲突解决策略

（1）链接法

（2）开放寻址法

a.线性探测：h(k, i) = (h'(k) + i) mod m

b.二次探测：h(k, i) = (h'(k) + c1i + c2 i^2) mod m

c.双重散列：h(k, i) = (h1(k) + i * h2(k)) mod m

（3）完全散列：设计一个较小的二次散列表

二、代码

代码中用到了函数指针，函数指针的用法参考函数指针总结

//Hash.h
#include <iostream>
using namespace std;

int m, NIL = 0;
//11.4 开放寻址法
typedef int (*Probing)(int k, int i);
int h(int k)
{
    return k % m;
}
int h2(int k)
{
    return 1 + k % (m-1);
}
//线性探测
int Linear_Probing(int k, int i)
{
    return (h(k) + i) % m;
}
//二次探测
int Quadratic_Probint(int k, int i)
{
    int c1 = 1, c2 = 3;
    return (h(k) + c1 * i + c2 * i * i) % m;
}
//双重探测
int Double_Probint(int k, int i)
{
    return (h(k) + i * h2(k)) % m;
}
int Hash_Insert(int *T, int k, Probing p)
{
    int i = 0, j;
    do{
        j = p(k, i);
        if(T[j] == NIL)
        {
            T[j] = k;
            return j;
        }
        i++;
    }
    while(i != m);
    cout<<"error:hash table overflow"<<endl;
}

int Hash_Search(int *T, int k, Probing p)
{
    int i = 0, j;
    while(1)
    {
        j = p(k, i);
        if(T[j] == NIL || i == m)
            break;
        if(T[j] == k)
            return j;
        i++;
    }
}