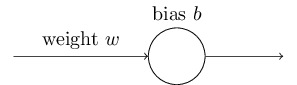
引入cross-entropy代价函数

定义一个神经元上的cross-entropy代价函数为：

问：为什么说C是一个代价函数？

答：1. C > 0 2. 当a接近y时C接近0

问：为什么cross-entropy代价函数能解决"learning slow down"的问题？

答：已知

$$a = \sigma(z) 是sigmoid函数 \\ z = \sum_jw_jx_j + b\\ \sigma'(z) = \sigma(z)(1-\sigma(z))$$

求C对w和b的偏导得：

可见，w和b的偏导与$\sigma'(z)$无关，只与y-a的差异有关。

使用cross-entropy作为代价函数对一个神经元的效果。

使用当前神经网络存在的问题中的同样的例子。 输入x = 1，期望输出 y = 0 令初始参数w=0.2， b=0.2，学习率eta=0.15，迭代效果如下： 可以看出，错误偏差越大学习速度越快。

将cross-entropy应用到整个神经网络

根据公式（63）可求出整个神经网络和w、b的偏导。

由公式可知，cross-entropy代价函数能解决整个神经网络的learn slowly的问题。

交叉熵代价函数 VS 二次代价函数

几乎所有的情况下交叉熵代价函数都要优于二次代价函数。

但当： 1. 输出层的神经元是线性神经元，即$a^L_j = z^L_j$时， 2. 代价函数为二次代价函数

时，可计算出w、b的偏导与使用cross-entropy代价函数得到的结果相同。