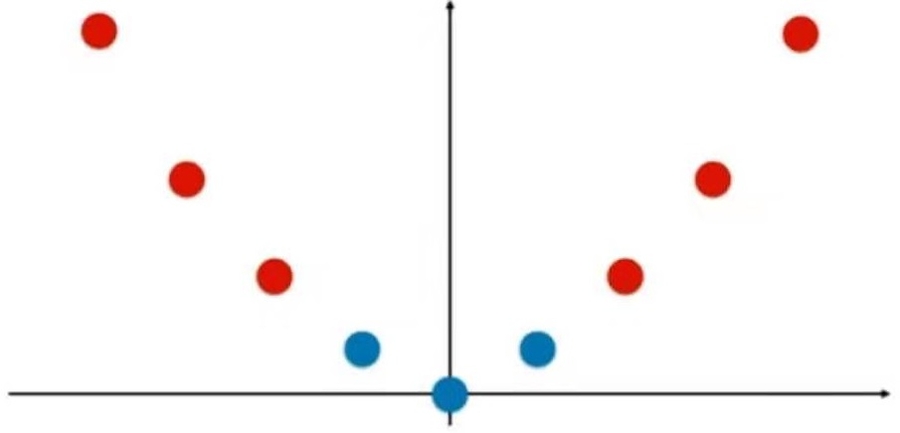
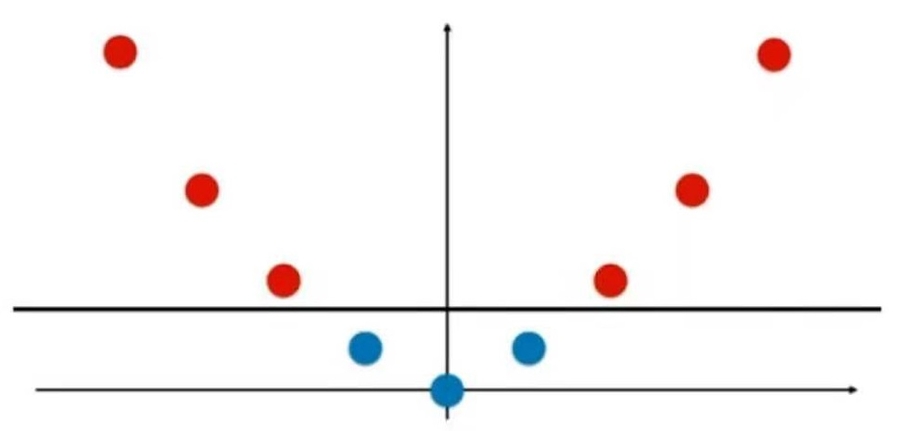
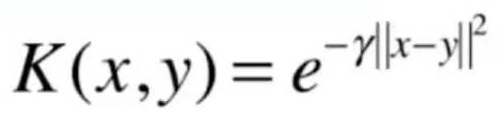11-7 高斯核函数
多项式特征为什么能处理线性不可分的问题?
使用高斯核函数升维
代码模拟高斯核函数的映射效果
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-4, 5, 1) # x = array([-4, -3, -2, -1, 0, 1, 2, 3, 4])
y = np.array((x>=-2) & (x<=2), dtype='int') # y = array([0, 0, 1, 1, 1, 1, 1, 0, 0])
plt.scatter(x[y==0], [0]*len(x[y==0]))
plt.scatter(x[y==1], [0]*len(x[y==1]))
plt.show()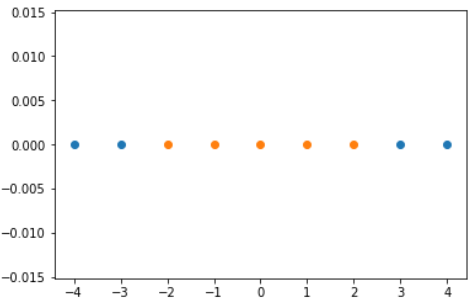
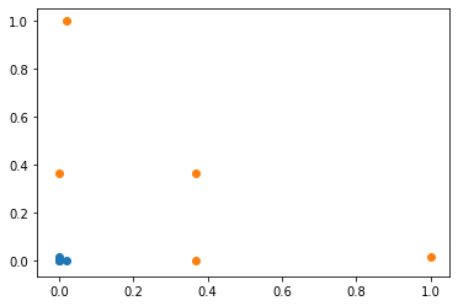
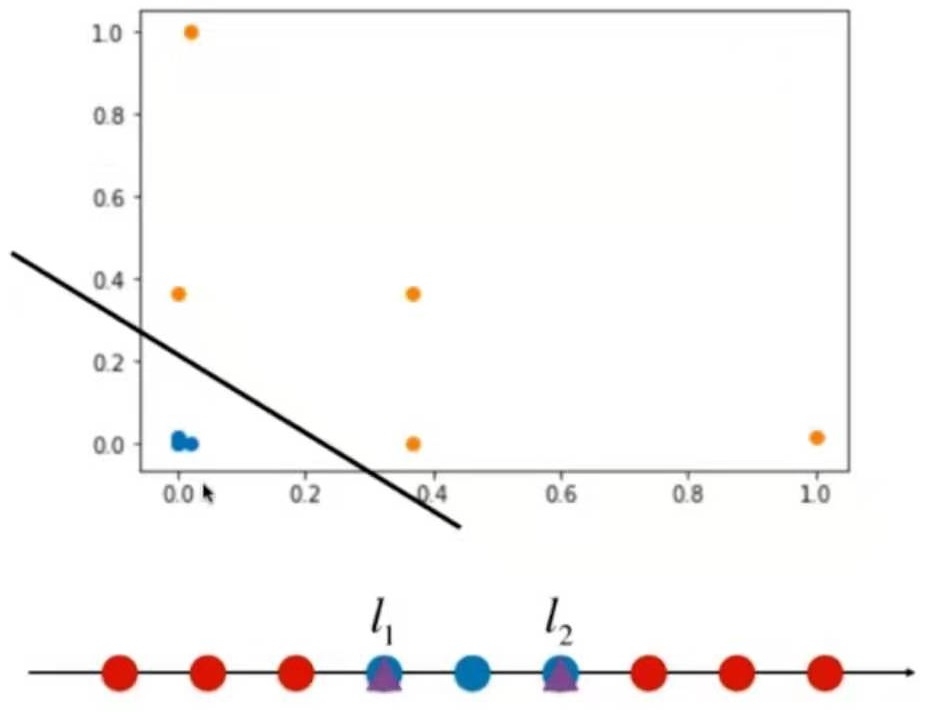
解释

Last updated