7-6 scikit learn中的PCA

沿用7-5中的测试数据，使用scikit-learn中的PCA

from sklearn.decomposition import PCA

pca = PCA(n_components=1)
pca.fit(X)

输入：pca.components_ 输出：array([[-0.75366744, -0.65725595]]) 这个轴与7-5中的计算结果是相反的。因为scikit-learn中不是什么梯度下降法而是什么数学方法计算的。 轴的方向相反不影响算法的结果

对比原始数据与降维再恢复后的数据

X_reduction = pca.transform(X)
X_restore = pca.inverse_transform(X_reduction)

plt.scatter(X[:, 0], X[:, 1], color='b', alpha=0.5)
plt.scatter(X_restore[:, 0], X_restore[:, 1], color='r', alpha=0.5)
plt.show()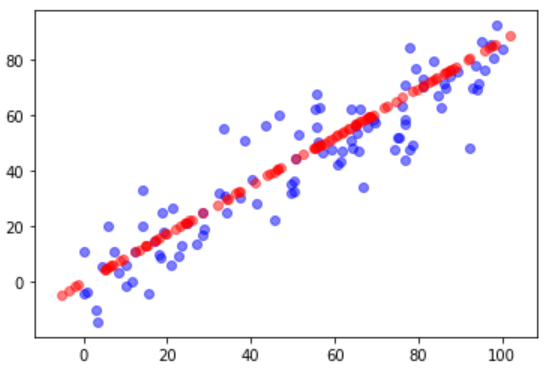

使用真实数据测试PCA降维对效率和准确度的影响

真实数据

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

digits = datasets.load_digits()
X = digits.data
y = digits.target

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

几种降维结果比较

PCA后的维数	运行时间	score
不降维	82.9 ms	0.9866666666666667
2	2.2	0.6066666666666667
28	1，05 时间更少了？	0.98

结论： 如果n_components选择合适，会大大减少训练时间而略微减少分类准确度，这样做是值得的。

选择合适的降维效果

确定新坐标系中每个维度保存了原数据的方差百分比

pca = PCA(n_components=X_train.shape[1])
pca.fit(X_train)
pca.explained_variance_ratio_

输出结果：

plt.plot([i for i in range(X_train.shape[1])],
    [np.sum(pca.explained_variance_ratio_[:i+1]) for  i in range(X_train.shape[1])])
plt.show()

输出结果： 这张图表示了前N个维度所占方差的百分比

保留原始数据95%的方差

pca = PCA(0.95)
pca.fit(X_train)
pca.explained_variance_ratio_

对原始数据降至2维的结果也有一定参考意义

pca = PCA(n_components=2)
pca.fit(X)
X_reduction = pca.transform(X)

for i in range(10):
    plt.scatter(X_reduction[y==i, 0], X_reduction[y==i,1], alpha=0.8)
plt.show()

假如只是要区分图中紫色的数据和红色的数据，降到2维就足够了