8-8 模型正则化 Regularization
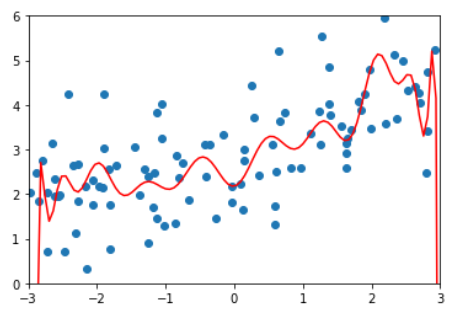
一个过拟合的例子:

岭回归 Ridge Regularization
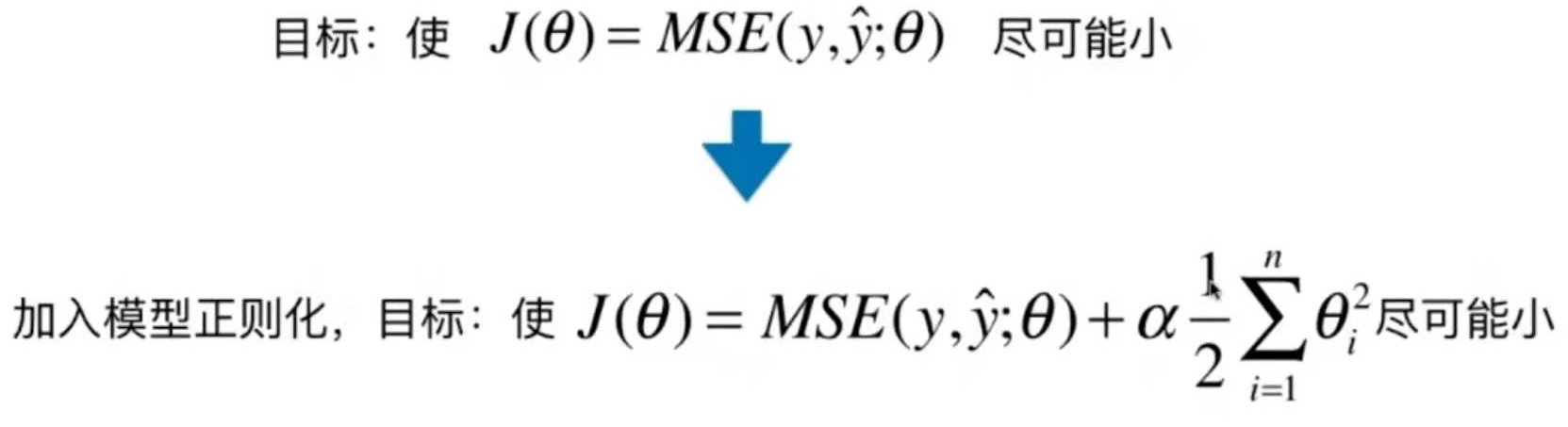
代码实现
测试数据

多项式回归,degree = 20
训练模型
绘制模型
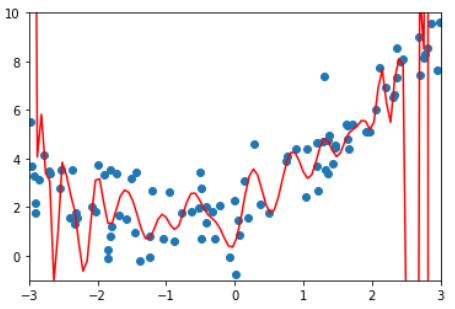
训练效果

岭回归,degree=20, alpha = 0.0001
训练模型
训练效果
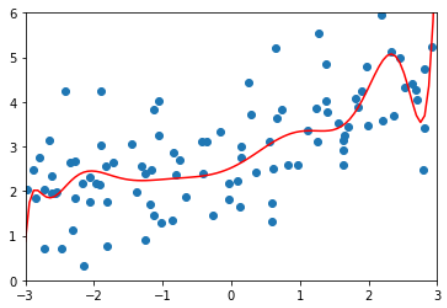
多项式回归及岭回归不同参数的训练结果比较
Last updated