8-3 过拟合和欠拟合

准备数据

import numpy as np
import matplotlib.pyplot as plt

x = np.random.uniform(-3, 3, size=100)
X = x. reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)

使用线性回归

from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X, y)
lin_reg.score(X, y)    # score = 0.4953707811865009

y_predict = lin_reg.predict(X)
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r')
plt.show()
from sklearn.metrics import mean_squared_error

y_predict = lin_reg.predict(X)
mean_squared_error(y, y_predict)

均方误差为：3.0750025765636577

使用多项式回归

多项式回归算法

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression

def PolynomialRegression(degree):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lin_reg", LinearRegression())
    ])

degree = 2的多项式回归

poly2_reg = PolynomialRegression(degree=2)
poly2_reg.fit(X, y)
y2_predict = poly2_reg.predict(X)
mean_squared_error(y, y2_predict)   # 1.0987392142417856

y_predict = lin_reg.predict(X)
plt.scatter(x, y)
plt.plot(np.sort(x), y2_predict[np.argsort(x)], color='r')
plt.show()

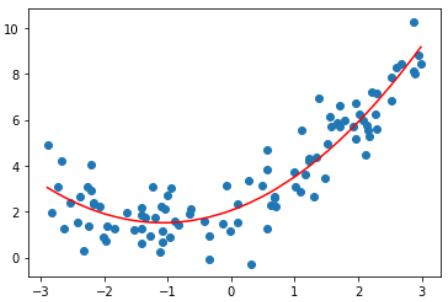
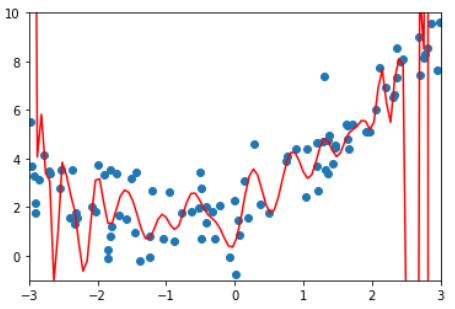
degree取不同值得到的均方误差和拟合结果

这张图不是特别准确，因为这根曲线只是原有数据点连接出来的结果. 因为有些x点取不到，不能准确描述所有点的y值， 均匀取值x并绘制图像如下

显示这不是我们想要的曲线。

结论：degree越高，对训练样本的拟合越好。 因为当degree足够大，总能找到一根曲线拟合所有的样本点，使得均方误差为0. 虽然拟合结果的均方误差小了，但它并没有真的反应样本点的曲线走势。 它为了拟合所有给定的样本而变得太过复杂，这就是过拟合(over fitting) 相反，如果只是使用一根直线来拟合样本数据，也没有很好的拟合样本的特征。 但它不是太复杂了，而是太简单了，这就是欠拟合(under fitting)

PreviousChapter8NextChapter8

Last updated