9-8 OvR与OvO
使用LogisticRegression提供的ovr和ovo
加载数据
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data[:, :2]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)OvR

OvO
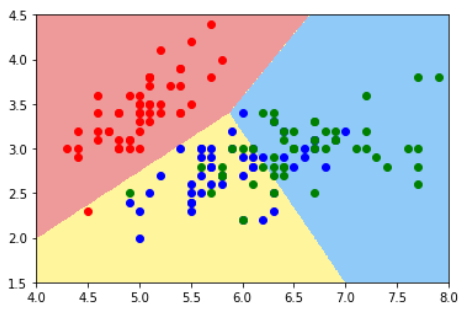
使用所有数据
使用scikit-learn中的OvR和OvO,能把所有二分类算法转换成多分类算法
Last updated

