> For the complete documentation index, see [llms.txt](https://windmising.gitbook.io/liu-yu-bo-play-with-machine-learning/llms.txt). Markdown versions of documentation pages are available by appending `.md` to page URLs; this page is available as [Markdown](https://windmising.gitbook.io/liu-yu-bo-play-with-machine-learning/src/chapter8-5/8-5.md).

# 8-5 学习曲线

![](http://windmissing.github.io/images/2019/129.jpg)\
这是8-4中提到的模型复杂度曲线。用于说明过拟合和欠拟合。\
还有另一种曲线，也可以可视化地表达过拟合与欠拟合的情况，即学习曲线。

## 学习曲线

随着训练样本的逐渐增多，算法训练出的模型的表现能力。

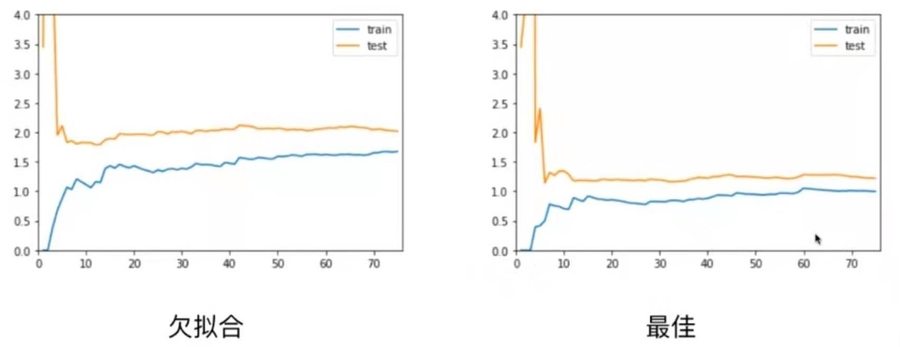
## 欠拟合、拟合、过拟合和学习曲线图对比

仍使用8-4中的数据

绘制学习曲线的函数如下：

```python
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

def plot_learning_curve(algo, X_train, X_test, y_train, y_test):
    train_score = []
    test_score = []
    for i in range(1, len(X_train)+1):
        algo.fit(X_train[:i], y_train[:i])
        y_train_predict = algo.predict(X_train[:i])
        train_score.append(mean_squared_error(y_train[:i], y_train_predict))
        y_test_predict = algo.predict(X_test)
        test_score.append(mean_squared_error(y_test, y_test_predict))

    plt.plot([i for i in range(1, len(X_train)+1)], np.sqrt(train_score), label="train")
    plt.plot([i for i in range(1, len(X_train)+1)], np.sqrt(test_score), label="test")
    plt.legend()
    plt.axis([0, len(X_train)+1, 0, 4])
    plt.show()
```

### 线性回归，欠拟合

```python
plot_learning_curve( LinearRegression(), X_train, X_test, y_train, y_test)
```

![](http://windmissing.github.io/images/2019/130.png)

在训练数据集上，误差逐渐升高。\
刚开始，误差累积较快，到后面误差累积变慢。\
在测试数据集上，刚开始误差很大，逐渐减小，减小到一定程度后达到相对稳定。\
最终，训练误差与测试误差趋于大体相同。测试误差略高于训练误差。

### 2阶多项式回归，拟合

```python
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression

def PolynomialRegression(degree):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lin_reg", LinearRegression())
    ])

plot_learning_curve( PolynomialRegression(degree=2), X_train, X_test, y_train, y_test)
```

![](http://windmissing.github.io/images/2019/131.png)

整体趋势与使用线性回归的图像是一致的。\
区别在于，线性回归模型中训练误差和测试误差稳定在1.7左右\
而2阶多项式回归模型中训练误差和测试误差稳定在1.0左右\
这说明使用2阶多项式回归的结果是比较好的。

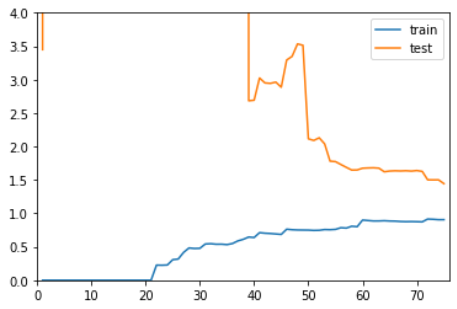
### 20阶多项式回归，过拟合

```python
plot_learning_curve( PolynomialRegression(degree=20), X_train, X_test, y_train, y_test)
```

![](http://windmissing.github.io/images/2019/132.png)

整体趋势仍然是train逐渐上升，test逐渐下降，最终趋于稳定。\
在区别是，在train和test都比较稳定时，它们之间的差距是比较大。\
这就说明模型虽然在训练数据集上拟合得非常好，但是在测试数据集上误差仍然很大。\
这种情况通常就是过拟合。

## 总结

![](http://windmissing.github.io/images/2019/133.jpg) 欠拟合情况和最佳情况相比，欠拟合情况train、test曲线趋于稳定的位置比最佳情况的要高一些。这是因为模型选择得不对，所以即使在训练数据集上误差也很大。 ![](http://windmissing.github.io/images/2019/134.jpg) 对于过拟合情况，train曲线和最佳情况差不多，但test曲线比较高，并且train与test之间的差距比较大。